Перегрузка операторов в руби и простая визуализация

November 20, 2012

Срочно в номер, срочно в номер. Ребята, оказывает в руби есть перегрузка операторов! Я работаю с руби уже несколько лет, а перегрузка есть! И у меня возникает ощущение, что она была все это время. Маловероятно, что ее добавили только вчера, когда я в первый раз про нее узнал.

Сегодня я покажу как можно облегчить реализацию простой математической визуализации фрактального типа, используя перегрузку стандартных операторов. Кроме того расскажу про удобные трансформации SVG, с которыми я также познакомился недавно.

Подготовим шаблон для генерации HTML-файла:

HTML_LAYOUT = <<-HTML
<!DOCTYPE html>
<html>
  <head><meta charset="utf-8"><title>Title</title></head>
  <style>body {text-align: center;}</style>
  <body>%body%</body>
</html>
HTML

В шаблон вставим SVG-картинку:

SIZE = 600.0 # размер SVG-картинки в пикселях

# Шаблон для генерации svg
SVG_TEMPLATE = <<-SVG
<svg xmlns="http://www.w3.org/2000/svg" version="1.1" width="#{SIZE.to_i}" height="#{SIZE.to_i}">
  <!--
    Подписи к координатным осям. Делаем здесь, так как иначе
    трансформации их перевернут.
  -->
  <text x="#{SIZE - 20}" y="#{SIZE/2 + 23}" font-family="Verdana" font-size="16" fill="black">X</text>
  <text x="#{SIZE/2 - 20}" y="#{20}" font-family="Verdana" font-size="16" fill="black">Y</text>


  <!--
    Транcформации приводят систему координат к привычной математической. Не нужно
    для отрисовки каждой точки выполнять преобразования координат (и ловить ошибки
    на этих преобразованиях).
  -->
  <g transform="translate(#{SIZE/2},#{SIZE/2})">
    <g transform="scale(-#{SIZE/3}, #{SIZE/3})">
      <g transform="rotate(180)">

        <!--
          Координатные оси. Они уже рисуются в привычном математическом масштабе от 0 до 1.
        -->
        <line x1="-1.5" y1="0" x2="1.5" y2="0" style="stroke:rgb(0,0,0);stroke-width:0.005" />
        <line x1="0" y1="-1.5" x2="0" y2="1.5" style="stroke:rgb(0,0,0);stroke-width:0.005" />

        <!--
          Отметки на осях [0, 1], [0, -1], [1, 0] и [-1, 0].
        -->
        <circle cx="0" cy="1" r="0.01" fill="black" />
        <circle cx="0" cy="-1" r="0.01" fill="black" />
        <circle cx="1" cy="0" r="0.01" fill="black" />
        <circle cx="-1" cy="0" r="0.01" fill="black" />

        <!-- Сам контент -->
        %content%
      </g>
    </g>
  </g>
</svg>
SVG

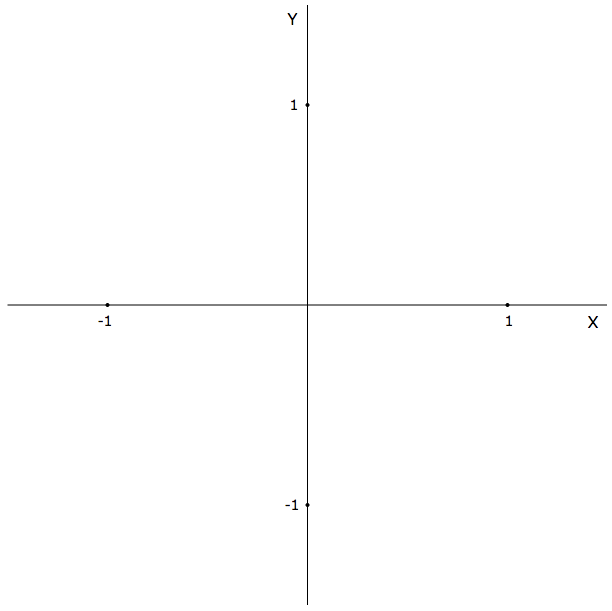
C помощью 3-х SVG-трансформаций мы подготовили привычную систему координат от -1.5 до 1.5, в которой удобно рисовать всякие математические и вероятностные штуки.

Далее создаем класс Vector (вот она перегрузка пошла):

# Вектор
class Vector < Struct.new(:x, :y)
  def +(other)
    Vector.new(x + other.x, y + other.y)
  end

  def *(factor)
    Vector.new(x*factor, y*factor)
  end

  def rotate(radians)
    Vector.new(
      x*Math.cos(radians) - y*Math.sin(radians),
      x*Math.sin(radians) + y*Math.cos(radians)
    )
  end

  def abs
    Math.sqrt(x*x + y*y)
  end
end

И рисуем три красных тентакля, используя новоиспеченную векторную математику в полном объеме:

File.open("out.html", "w") do |f|
  f.puts HTML_LAYOUT.sub('%body%'){
    SVG_TEMPLATE.sub('%content%') {
      out = ""
      point = Vector.new(0, 0)
      scale = Vector.new(0.079, 0)
      150.times.each do |i|
        point2 = point.rotate(Math::PI*2/3)
        point3 = point.rotate(Math::PI*4/3)
        out += %(<circle cx="#{point.x}" cy="#{point.y}" r="0.02" fill="red" />)
        out += %(<circle cx="#{point2.x}" cy="#{point2.y}" r="0.02" fill="red" />)
        out += %(<circle cx="#{point3.x}" cy="#{point3.y}" r="0.02" fill="red" />)
        point += scale                    # <-- Вот она перегрузка
        scale = (scale*0.98).rotate(0.1)  # <-- и здесь
      end
      out
    }
  }
end

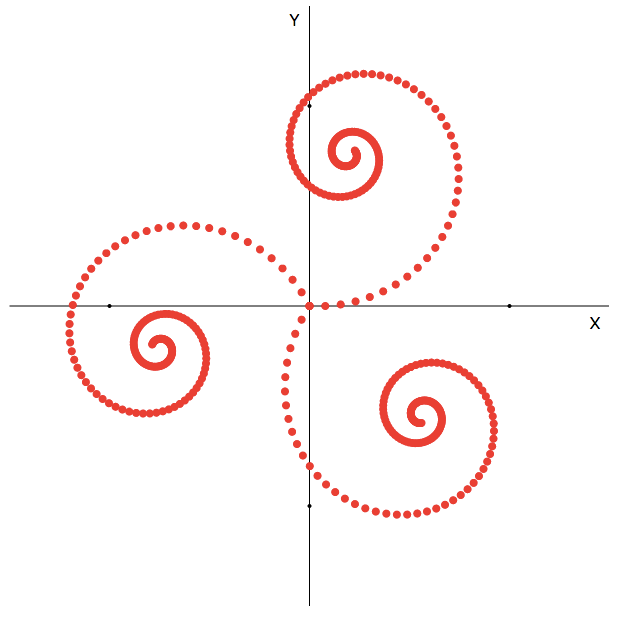
Красиво и просто (математические объекты - это самое красивое, что могут сделать программисты без дизайнеров):

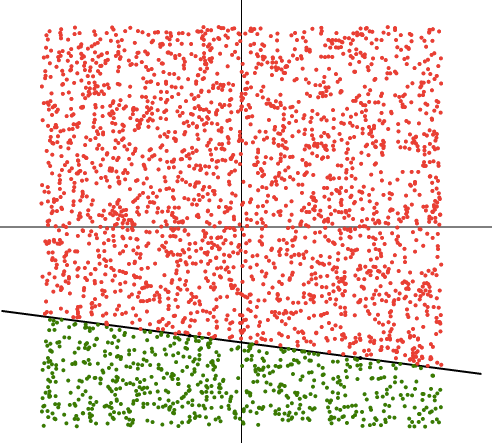
Счастливой визуализации! Напоследок еще картинка, которую я нарисовал, используя данную технологию, решая одну задачу из теории вероятности: